Bending plates of nematic liquid crystal elastomers

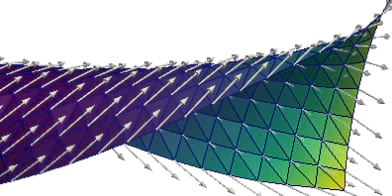
Programmable actuators are devices made of elastic materials whose shape can be controlled via external stimulation. Because of a wide range of technological applications particularly at small scales, they have received considerable attention in engineering, physics, and applied mathematics. A precise understanding of their behavior is crucial for their design and reliable use. This requires effective mathematical models and accurate numerical simulation methods. The proposed project focusses on the class of nematic thin films which are thin sheets of nematic liquid crystal elastomers. Starting from a coupled model using the frameworks of 3D hyperelasticity, and liquid crystal models (e.g., Oseen-Frank), different effective two-dimensional plate models will be derived that determine a possibly large deformation of the elastic thin film in connection with a corresponding orientation field describing the arrangement of the liquid crystals. Characteristic for the models are the occurrence of curvature quantities, constraints that enforce ruled surfaces, vector fields of unit or bounded length, and nonlinearities that define the coupling between the two quantities of interest. These special features require the use and development of appropriate numerical methods in order to simulate relevant effects within efficient implementations and to make reliable predictions for the development of new nanotools. A mathematically rigorous connection between the three-dimensional and the dimensionally reduced nonlinear plate bending model will be established via the concept of Gamma-convergence, a thorough convergence analysis for the proposed finite element discretization will be carried out avoiding unjustified regularity assumptions, and efficient iterative solution strategies will be investigated theoretically and experimentally.

Project group

• Prof. Dr. Sören Bartels
• Prof. Dr. Stefan Neukamm
• Max Griehl
• Christian Palus

Publications

Sören Bartels, Chapter 3 - Finite element simulation of nonlinear bending models for thin elastic rods and plates, In Geometric partial differential equations. Part I (Elsevier/North-Holland, Amsterdam), 2020. [doi] [bibtex]

Sören Bartels, Numerical simulation of inextensible elastic ribbons, In SIAM Journal on Numerical Analysis, Vol. 58 (6), pp. 3332–3354, 2020. [doi] [bibtex]

Sören Bartels and Philipp Reiter, Numerical solution of a bending-torsion model for elastic rods, In Numerische Mathematik, Vol. 146 (4), pp. 661–697, 2020. [doi] [bibtex]

Harbir Antil, Sören Bartels, and Armin Schikorra, Approximation of fractional harmonic maps, In IMA Journal of Numerical Analysis, 2022, drac029. [doi] [bibtex]

Sören Bartels and Philipp Reiter, Stability of a simple scheme for the approximation of elastic knots and self-avoiding inextensible curves, In Mathematics of Computation, Vol. 90, pp. 1499–1526, 2021. [doi] [bibtex]

Sören Bartels and Christian Palus, Stable gradient flow discretizations for simulating bilayer plate bending with isometry and obstacle constraints, In IMA Journal of Numerical Analysis, 2021, drab050. [doi] [bibtex]

Sören Bartels, Frank Meyer, and Christian Palus, Simulating Self-Avoiding Isometric Plate Bending, In SIAM Journal on Scientific Computing, Vol. 44 (3), pp. A1475–A1496, 2022. [doi] [bibtex]

Sören Bartels, Max Griehl, Stefan Neukamm, David Padilla-Garza, and Christian Palus, A nonlinear bending theory for nematic LCE plates, In Mathematical Models and Methods in Applied Sciences, pp. 1–80, 2023. [doi] [bibtex]

Sören Bartels, Max Griehl, Jakob Keck, and Stefan Neukamm, Modeling and simulation of nematic LCE rods, arXiv e-prints, 2205.15174 [math.AP], 2022. [bibtex]

Sören Bartels, Klaus Böhnlein, Christian Palus, and Oliver Sander, Benchmarking Numerical Algorithms for Harmonic Maps into the Sphere, arXiv e-prints, 2209.13665 [math.NA], 2022. [bibtex]

Sören Bartels, Christian Palus, and Zhangxian Wang, Quasi-Optimal Error Estimates for the Finite Element Approximation of Stable Harmonic Maps with Nodal Constraints, In SIAM Journal on Numerical Analysis, Vol. 61, pp. 1819–1834, 2023. [doi] [bibtex]