Vector- and Tensor-Valued Surface PDEs

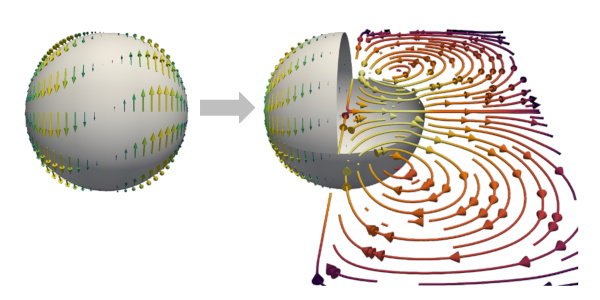
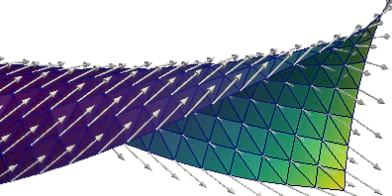
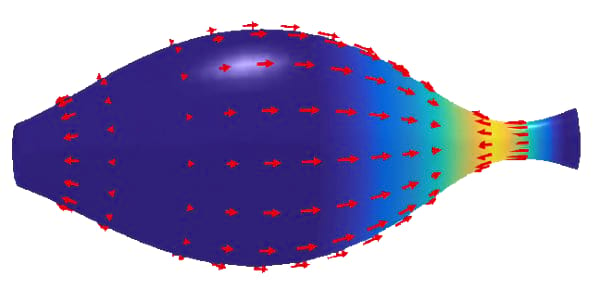
Most of the work on PDEs that are defined on curved surfaces is concerned with scalar-valued equations. In this case the coupling between surface geometry and the PDE is weak, and thus numerical approaches established in flat spaces are applicable after small modifications. For vector- and tensor-valued surface PDEs these approaches are no longer sufficient. The surface vector- and tensor-fields need to be considered as elements of the tangent bundle, and thus the coupling between surface geometry and the PDE becomes more severe. Progress on this topic is currently made in different communities and in the course of studying specific problems from different application areas, including fluid dynamics, materials science, mechanics, and biophysics.

The research unit establishes a scientific platform that brings together experts from different areas, in particular, mathematical modeling, numerical analysis and simulation, with different perspectives on vector- and tensor-valued surface PDEs, and will contribute to a deeper understanding of the mathematical challenges in the field by investigating specific problems in different application areas. The models studied in the research unit address problems in biophysics and mechanics and range from fluidic membranes, topological active matter and a description of viscoelastic properties of a cell cortex, to slender prestrained elastic structures and plates of nematic liquid crystal elastomers. All of these topics are by itself highly active fields of research, in which predictive and reliable simulations are believed to catalyze further developments. Models for these problems involve vector- and tensor-valued surface PDEs and feature a nonlinear structure that is imposed by the geometry of the surface.