Active gels on surfaces

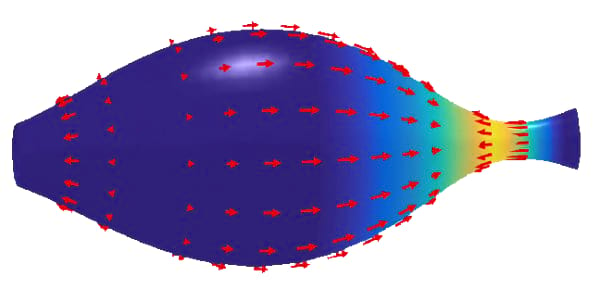
Active polar and nematic gels on surfaces embody a tight coupling between topology, geometry, deformation, and hydrodynamics. This coupling is hypothesized to be essential for morphogenetic processes in living systems. In this project, we will derive the model equations by two different approaches: a thin-film limit of established 3D active gel models, as well as intrinsic balance laws. The correct coupling between surface deformation in the normal direction and internal fluid properties, such as orientational and flow fields, is going to be of particular importance. The issue of how to transport vector (director) fields and tensor (Q-tensor) fields on evolving surfaces will be addressed. Numerically, we tackle the problem by comparing continuous particle methods with surface finite-element approaches. Due to the complexity of the equations, only parts can be addressed analytically in cooperation with project Reusken/Voigt. Therefore, we provide validation by quantitatively comparing two numerical methods and by qualitative comparison with experimental results. Close cooperations exist with projects Reusken/Voigt and Bartel/Neukamm for modeling hydrodynamics and liquid crystals, respectively, and their coupling with surface shape changes.

Project group

• Prof. Dr. Ivo Sbalzarini
• Prof. Dr. Axel Voigt
• Veit Krause
• Alejandra M. Foggia

Publications

Michael Rank and Axel Voigt, Active flows on curved surfaces, In Physics of Fluids, Vol. 33, pp. 072110, 2021. [doi] [bibtex]

Ingo Nitschke, Sebastian Reuther, and Axel Voigt, Liquid crystals on deformable surfaces, In Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol. 476 (2241), pp. 20200313, 2020. [doi] [bibtex]

Ingo Nitschke and Axel Voigt, Observer-invariant time derivatives on moving surfaces, In Journal of Geometry and Physics, Vol. 173, pp. 104428, 2022. [doi] [bibtex]

Elena Bachini, Philip Brandner, Thomas Jankuhn, Michael Nestler, Simon Praetorius, Arnold Reusken, and Axel Voigt, Diffusion of tangential tensor fields: numerical issues and influence of geometric properties, arXiv e-prints, 2205.12581 [math.NA], 2022. [bibtex]