Projects of funding period 1

All five projects consider essential aspects of vector- and tensor-valued surface PDEs and all address modeling as well as numerical issues. The problems considered range from surface fluids to thin elastic structures and from academic benchmark problems to real applications. The individual projects are summarized below.

• Numerical methods for surface fluids

  

  In this project we consider a class of surface Navier-Stokes equations which are used to model viscous two-dimensional incompressible fluids on surfaces. We restrict to sufficiently smooth closed oriented (evolving) surfaces embedded in $\mathbb{R}^3$ . For stationary surfaces or evolving surfaces with a prescribed normal velocity the surface Navier-Stokes equations proposed in the literature have different representations but can be shown to be (formally) eq... Read More

• Active Rheology/Mechanics of active Biomaterials

  

  The actin cortex in conjunction with the cell membrane is a thin film that encloses the viscous interior of most animal cells. The actin cortex is a complex viscoelastic material which exhibits active prestress due to inherent microscopic force-dipoles constituted by molecular myosin motor proteins. Observations of cells show that the actin cortex film can form self-organized patterns and actively deform itself. The cortex is thus a key regulator for the emergence of cell shape and vital f... Read More

• Heterogeneous thin structures with prestrain

  

  Prestrain and -stress can have a tremendous effect on the mechanical behavior of slender elastic structures leading to, e.g., complex shapes in equilibrium, wrinkling and symmetry breaking. Natural and synthetic materials (including biomembranes as considered in other projects in the research unit) feature residual stress due to growth, swelling, or thermal expansion. These mechanisms are used in the design of active films and rods that undergo a change of shape triggered by an external st... Read More

• Bending plates of nematic liquid crystal elastomers

  

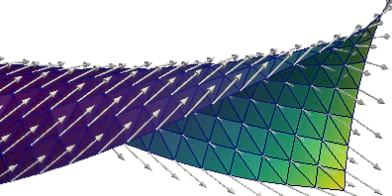
  Programmable actuators are devices made of elastic materials whose shape can be controlled via external stimulation. Because of a wide range of technological applications particularly at small scales, they have received considerable attention in engineering, physics, and applied mathematics. A precise understanding of their behavior is crucial for their design and reliable use. This requires effective mathematical models and accurate numerical simulation methods. The proposed project focus... Read More

• Active gels on surfaces

  

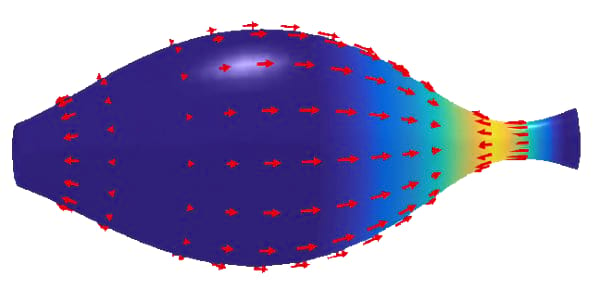
  Active polar and nematic gels on surfaces embody a tight coupling between topology, geometry, deformation, and hydrodynamics. This coupling is hypothesized to be essential for morphogenetic processes in living systems. In this project, we will derive the model equations by two different approaches: a thin-film limit of established 3D active gel models, as well as intrinsic balance laws. The correct coupling between surface deformation in the normal direction and internal fluid properties, ... Read More